.jpg?1751458741)
4th International Electronic Conference on Entropy and Its Applications
Part of the International Conference on Entropy and Its Applications series
21 November–1 December 2017
- Go to the Sessions
- Event Details
Welcome from the Chairs
21 November-1 December 2017 |
Welcome from the Chair of the 4th ECEA
You are cordially invited to participate in the 4th International Electronic Conference on Entropy and Its Applications. Building on the success of the past three events in this sequence, the conference is designed to bring together researchers working in the field, to present and discuss their recent contributions, without needing to leave the comfort of their home.
Conserved quantities such as energy, and monotonic quantities such as entropy, are fundamental to our understanding of high-dimensional dynamical systems. Since the foundations of irreversibility were laid in 19th century thermodynamics, and the conceptual analogy between statistical mechanics and information theory (both classical and quantum) was made in the 20th century, inter-related concepts of entropy have been fruitfully applied to a large and expanding list of fields, including economics, biology, computer science, operations research using maximum entropy estimates, linguistics and the social sciences.
The conference will be organized into six sessions, which reflect the inter-disciplinary nature of entropy and its applications:
- Section A
- Statistical Physics: Statistical Mechanics, Irreversibility, Fluctuation Theorems, Equilibrium and Non-Equilibrium Distributions, Phase Transitions, Stochastic Systems, Chaos and Nonlinear Dynamics, Population Dynamics and Genetics
- Section B
- Information and Complexity: Simplicity and Complexity, Shannon Entropy, Kullback–Leibler Divergence, Channel Capacity, Alternative Entropies, Coding, Operations Research, Forecasting, Symmetry Breaking, Similarity
- Section C
- Thermodynamics in Materials: Chemical thermodynamics, the Second Law, Free Energy, Enthalpy, Self-Organization, Biochemical Networks, Nano-Scale Physics, Molecular Theory of Fluids
- Section D
- Quantum Information and Foundations: Quantum Foundations, Quantum Probability and non-Kolmogorov Models, Quantum-Like Models in Cognition, Decision Making, Psychology, Social and Political Science, Economics and Finances, Bell's Inequality, Quantum Nonlocality, Contextuality, Pure and Mixed States, Superposition, De-coherence, Quantum Computing, Born Rule and Generalizations, Causality and Randomness, Role of Conscious Observer
- Section E
- Machine Learning: Artificial Intelligence, Neural Networks, Cybernetics, Robotics, Man–Machine Interfaces, Bio-mimic Algorithms
- Section F
- Astrophysics and Cosmology: Evolution of Stars, Gravitating Systems, Black Holes, The Universe
- Section P
- Posters: Posters can be presented stand-alone, i.e., without an accompanying proceedings paper or conference presentation. Posters will be available online on this website during and after the e-conference. However, posters will not be added to the proceedings of the conference.
Accepted papers will be published in the proceedings of the conference, and selected/extended papers will be considered for publication in Entropy with a 20% discount off the APC. Entropy is an open access publication journal of MDPI in the field of entropy and information theory.
Conference Chair
|
Editorial Board of the Journal Entropy Department of Mathematics and Statistics |
 |
Section Chairs
Dr. Antonio M. Scarfone (Politecnico di Torino, Torino, Italy)
Prof. Dr. Miguel Rubi (Universitat de Barcelona, Barcelona, Spain)
Prof. Dr. Raúl Alcaraz Martínez (University of Castilla-La Mancha, Cuenca, Spain)
Dr. Dawn E. Holmes (University of California, Oakland, CA, USA)
Prof. Dr. Alexander Gorban (University of Leicester, Leicester, UK)
Dr. Andriy Olenko (La Trobe University, Melbourne, Australia)
Prof. Dr. Leslie Glasser (Curtin University, Perth, Australia)
Prof. Giacomo Mauro D'Ariano (University of Pavia, Pavia, Italy)
Prof. Dr. Andrei Khrennikov (Linnaeus University, Växjö, Sweden)
Dr. Michael J. Way (NASA Goddard Institute for Space Studies, New York, NY, USA)
Scientific Advisory Committee Members
| Prof. Anne Humeau-Heurtier (University of Angers, Angers cedex, France) Dr. Takuya Yamano (Kanagawa University, Kanagawa, Japan) Prof. Dr. Carlo Cattani (Engineering School (DEIM) University of Tuscia, Viterbo, Italy) Dr. Renaldas Renaldas Urniezius (Kaunas University of Technology, Lithuania) Dr. Robert Niven (The University of New South Wales at ADFA, Canberra, Australia) |
Confirmed Keynote Speakers
|
|
|
|
|
|
|
|
|
|
|
|
Conference Secretariat
Ms. Connie XiongMs. Cecilia Yang
E-mail: ecea@mdpi.com or entropy@mdpi.com
Call for Papers
The section Chairs and the scientific committee members are pleased to announce the Call for Papers for the 4th International Electronic Conference on Entropy and Its Applications and to invite each researcher working in this exciting field of science to share his/her recent results with his/her colleagues around the world.
The conference will be organized into six sections, which reflect the inter-disciplinary nature of entropy and its applications. It will cover a wide range of aspects, please see the details in each section.
Researchers are invited to provide a short abstract on line at https://www.sciforum.net/login from now until 20 October 2017. Acceptance will be notified within a week after submission of the abstract. Then the author(s) will be asked to submit the manuscript, optionally along with a slide show (PPT) (or a video) using the template provided by the conference (see Instructions for Authors). All accepted submissions will be displayed online, at https://sciforum.net/conference/ecea-4, for discussion during 21 November–1 December 2017.
Accepted papers will be published in the Journal Proceedings. After the conference, the authors are recommended to submit an extended version of the proceeding papers to the Entropy Special issue with 20% discount of the APC charges.
The Scientific Committee looks forward to receiving contributions in response to this call and will be glad to provide any further information to interested parties. Questions may be addressed to the Entropy editorial office at ecea@mdpi.com or entropy@mdpi.com.
We thank you in advance for your attendance of this conference and look forward to a stimulating exchange.
Conference Chairs
P.Broadbridge@latrobe.edu.au
Instructions for Authors
Submissions should be done by the authors online by registering with www.sciforum.net, and using the "Start New Submission" function once logged into system.
- Scholars interested in participating with the conference can submit their abstract (about 200-250 words covering the areas of manuscripts for the proceedings issue) online on this website until 6 October 2017.
- The Conference Committee will pre-evaluate, based on the submitted abstract, whether a contribution from the authors of the abstract will be welcome for the 4th International Electronic Conference on Entropy and Its Applications. All authors will be notified by 20 October 2017 about the acceptance of their abstract.
- If the abstract is accepted for this conference, the author is asked to submit the manuscript, optionally along with a PowerPoint and/or video presentation of his/her paper (only PDF), until the submission deadline of 3 November 2017.
- The conference proceedings papers and presentations will be available on https://sciforum.net/conference/ecea-4 for discussion during the time of the conference 21 November–1st December 2017.
- Accepted papers will be published in the Journal Proceedings. After the conference, the authors are recommended to submit an extended version of the proceeding papers to the Entropy Special issue with 20% discount of the APC charges.
Manuscripts for the proceedings issue must have the following organization:
First page:
- Title
- Full author names
- Affiliations (including full postal address) and authors' e-mail addresses
- Abstract
- Keywords
- Introduction
- Methods
- Results and Discussion
- Conclusions
- (Acknowledgements)
- References
Manuscripts should be prepared in MS Word or any other word processor and should be converted to the PDF format before submission. The publication format will be PDF. The manuscript should count at least 3 pages (including figures, tables and references). There is no page limit on the length, although authors are asked to keep their papers as concise as possible.
Authors are encouraged to prepare a presentation in PowerPoint or similar software, to be displayed online along with the Manuscript. Slides, if available, will be displayed directly in the website using Sciforum.net's proprietary slides viewer. Slides can be prepared in exactly the same way as for any traditional conference where research results can be presented. Slides should be converted to the PDF format before submission so that our process can easily and automatically convert them for online displaying.
Besides their active participation within the forum, authors are also encouraged to submit video presentations. If you are interested in submitting, please contact the conference organizer (ecea@mdpi.com) to get to know more about the procedure. This is an unique way of presenting your paper and discuss it with peers from all over the world. Make a difference and join us for this project!
Posters will be available on this conference website during and after the event. Like papers presented on the conference, participants will be able to ask questions and make comments about the posters. Posters that are submitted without paper will not be included in the proceedings of the conference.
Submission: Manuscripts should be submitted online at www.sciforum.net/login by registering and logging in to this website.
Accepted File Formats
- MS Word: Manuscript prepared in MS Word must be converted into a single file before submission. When preparing manuscripts in MS Word, the 4th Electronic Conference on Entropy and Its Applications Microsoft Word template file (see download below) must be used. Please do not insert any graphics (schemes, figures, etc.) into a movable frame which can superimpose the text and make the layout very difficult.
Electronic Conference on Entropy and Its Applications Microsoft Word template file
- LaTeX: Ensure to send a copy of your manuscript as a PDF file also, if you decided to use LaTeX. When preparing manuscripts in LaTeX, please use the MDPI LaTeX template files.
Electronic Conference on Entropy and Its Applications LaTeX template file
- Paper Format: A4 paper format, the printing area is 17.5 cm x 26.2 cm. The margins should be 1.75 cm on each side of the paper (top, bottom, left, and right sides).
- Formatting / Style: The paper style of the Journal Entropy should be followed. You may download the template file to prepare your paper. The full titles and the cited papers must be given. Reference numbers should be placed in square brackets [ ], and placed before the punctuation; for example [4] or [1-3], and all the references should be listed separately and as the last section at the end of the manuscript.
- Authors List and Affiliation Format: Authors' full first and last names must be given. Abbreviated middle name can be added. For papers written by various contributors a corresponding author must be designated. The PubMed/MEDLINE format is used for affiliations: complete street address information including city, zip code, state/province, country, and email address should be added. All authors who contributed significantly to the manuscript (including writing a section) should be listed on the first page of the manuscript, below the title of the article. Other parties, who provided only minor contributions, should be listed under Acknowledgments only. A minor contribution might be a discussion with the author, reading through the draft of the manuscript, or performing English corrections.
- Figures, Schemes and Tables: Authors are encouraged to prepare figures and schemes in color. Full color graphics will be published free of charge. Figure and schemes must be numbered (Figure 1, Scheme I, Figure 2, Scheme II, etc.) and a explanatory title must be added. Tables should be inserted into the main text, and numbers and titles for all tables supplied. All table columns should have an explanatory heading. Please supply legends for all figures, schemes and tables. The legends should be prepared as a separate paragraph of the main text and placed in the main text before a table, a figure or a scheme.
It is the authors' responsibility to identify and declare any personal circumstances or interests that may be perceived as inappropriately influencing the representation or interpretation of clinical research. If there is no conflict, please state here "The authors declare no conflict of interest." This should be conveyed in a separate "Conflict of Interest" statement preceding the "Acknowledgments" and "References" sections at the end of the manuscript. Financial support for the study must be fully disclosed under "Acknowledgments" section. It is the authors' responsibility to identify and declare any personal circumstances or interests that may be perceived as inappropriately influencing the representation or interpretation of clinical research. If there is no conflict, please state here "The authors declare no conflict of interest." This should be conveyed in a separate "Conflict of Interest" statement preceding the "Acknowledgments" and "References" sections at the end of the manuscript. Financial support for the study must be fully disclosed under "Acknowledgments" section.
CopyrightMDPI AG, the publisher of the Sciforum.net platform, is an open access publisher. We believe that authors should retain the copyright to their scholarly works. Hence, by submitting a Communication paper to this conference, you retain the copyright of your paper, but you grant MDPI AG the non-exclusive right to publish this paper online on the Sciforum.net platform. This means you can easily submit your paper to any scientific journal at a later stage and transfer the copyright to its publisher (if required by that publisher).
List of accepted submissions (33)
| Id | Title | Authors | Poster PDF | ||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sciforum-013909 | Using the entropy generation analysis in flow boiling conditions for enhanced heat transfer techniques : Micro-fin tube | , , , , | N/A |
Show Abstract |
|||||||||||||||||||||||||||||||||||||
|
The flow boiling heat transfer is one of the common phenomenon happens in the industries. The micro-fin tubes are one of the geometries in enhancing heat transfer rate in boiling condition. The entropy generation analysis is presented with its formulation precisely to find best operating conditions in micro-fin tubes in terms of changing in geometry and flow conditions. This analysis shows important aspects of losses in fluid systems when boiling happens. The losses include thermal loss related to the heat transfer and hydraulic one related to the pressure drop. The relevant terms are described for both of these losses. The optimum tube diameter under specified conditions is found. The effect of different flow conditions such as mass velocity, inlet vapor quality on contribution of pressure drop and heat transfer in entropy generation is discussed. It is found that, there is a desirable conditions of fluid flow and micro-fin geometrical shape to reach the minimum of entropy generation. |
|||||||||||||||||||||||||||||||||||||||||
| sciforum-013921 | Zeeman effects on the entanglement of non-equilibrium finite-spin systems | N/A |
Show Abstract |
||||||||||||||||||||||||||||||||||||||
|
We study the Zeeman effect on entanglement of non-equilibrium finite-spin systems with external fields using a method based on thermofield dynamics (TFD). For this purpose, the extended density matrices and extended entanglement entropies of two systems with either non-competing or competing external fields are calculated according to the dissipative von Neumann equation, and the numerical results are compared. Consequently, through the ``twin-peaks'' oscillations of the quantum entanglement, we have illustrated the Zeeman effect on the entanglement of non-equilibrium finite-spin systems with competing external fields in the TFD algorithm. |
|||||||||||||||||||||||||||||||||||||||||
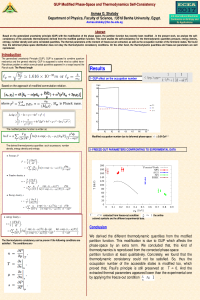
| sciforum-014019 | GUP Modified Phase-Space and Thermodynamics Self-Consistency |
|
Show Abstract |
||||||||||||||||||||||||||||||||||||||
|
Based on the generalized uncertainty principle (GUP) with the modi cation of the phase space, the partition function has recently been modi ed . In the present work, we analyze the self-consistency of the axiomatic thermodynamic derived from the modi ed partition function. This work studies the self-consistency for the thermodynamic quantities pressure, energy density, entropy, number density and some correlated quantities. The thermal parameters at the moment of freeze-out are extracted, as well as the occupation number of the fermionic states. We found that, the deformed phase space distribution does not obey the thermodynamic consistency conditions. On the other hand, the thermodynamic quantities and freeze-out parameters are well reproduced. |
|||||||||||||||||||||||||||||||||||||||||
| sciforum-014291 | Information Entropy of Molecular Tunneling | , |

|
Show Abstract |
|||||||||||||||||||||||||||||||||||||
|
Molecular tunneling process has been considered by means of radiation theory. The formula for information entropy calculation has been derived by means of interaction model of thermal equilibrium radiation with a molecule at low temperatures. The physical meaning of information entropy for low-temperature plateau of unimolecular chemical reaction has been determined. It is a measure of conversion of thermal radiation energy to mechanical energy that moves atoms in a molecule during elementary activation act. It is also a measure of uncertainty of this energy conversion. The conversion takes place at a temperature when the average energy of the elementary activation act is equal to a part of zero energy of the transforming molecule. Two unimolecular reactions have been investigated. These are Fe-CO bond recombination in β-hemoglobin and double proton transfer in benzoic acid dimer for sequential deuteration of hydrogen bond and various hydrostatic pressures. Using the information entropy formula it is possible to calculate its value in energy units of measurements for low-temperature plateau. Probabilities of occurrence of the reactions under considerations, their efficiency and mean-square fluctuations of the distribution function parameters have also been determined [1]. [1] A.V. Stepanov, International Journal of Modern Physics B, Vol. 29, No 4 (2015) 1550016 (18 pages). |
|||||||||||||||||||||||||||||||||||||||||
| sciforum-014322 | Interpolating Binary and Multivalued Logical Quantum Gates | , | N/A |
Show Abstract |
|||||||||||||||||||||||||||||||||||||
|
A method for synthesizing quantum gates is presented based on interpolation methods applied to operators in Hilbert space. Starting from the diagonal forms of specific generating seed operators with non-degenerate eigenvalue spectrum one obtains for arity-one a complete family of logical operators corresponding to all the one-argument logical connectives. Scaling-up to n -arity gates is obtained by using the Kronecker product and unitary transformations. The quantum version of the Fourier transform of Boolean functions is presented and a Reed-Muller decomposition for quantum logical gates is derived. The common control gates can be easily obtained by considering the logical correspondence between the control logic operator and the binary logic operator. A new polynomial and exponential formulation of the Toffoli gate is presented. The method has parallels to quantum gate-T optimization methods using powers of multilinear operator polynomials. The method is then applied naturally to alphabets greater than two for multi-valued logical gates used for quantum Fourier transform, min-max decision circuits and multivalued adders. |
|||||||||||||||||||||||||||||||||||||||||
Conference Schedule
- Abstract Submission: 6 October 2017 13 October 2017
- Notification of Acceptance: 20 October 2017
- Submission of Full Paper and Poster/Presentation: 3 November 2017
- Conference Open: 21 November–1 December 2017
Conference Organizers
- Chair of the 4th International Electronic Conference on Entropy and Its Applications
Prof. Dr. Philip Broadbridge
La Trobe University
Melbourne, Australia
Editorial Board of the Journal Entropy
- Section Chairs
Dr. Antonio M. Scarfone (Politecnico di Torino, Torino, Italy)
Prof. Dr. Miguel Rubi (Universitat de Barcelona, Barcelona, Spain)
Prof. Dr. Raúl Alcaraz Martínez (University of Castilla-La Mancha, Cuenca, Spain)
Dr. Dawn E. Holmes (University of California, Oakland, CA, USA)
Prof. Dr. Alexander Gorban (University of Leicester, Leicester, UK)
Dr. Andriy Olenko (La Trobe University, Melbourne, Australia)
Prof. Dr. Leslie Glasser (Curtin University, Perth, Australia)
Prof. Giacomo Mauro D'Ariano (University of Pavia, Pavia, Italy)
Prof. Dr. Andrei Khrennikov (Linnaeus University, Växjö, Sweden)
Dr. Michael J. Way (NASA Goddard Institute for Space Studies, New York, NY, USA)
- Scientific Advisory Committee
Prof. Anne Humeau-Heurtier (University of Angers, Angers cedex, France)
Dr. Takuya Yamano (Kanagawa University, Kanagawa, Japan)
Prof. Dr. Carlo Cattani (Engineering School (DEIM) University of Tuscia, Viterbo, Italy)
Dr. Renaldas Renaldas Urniezius (Kaunas University of Technology, Lithuania)
Dr. Robert Niven (The University of New South Wales at ADFA, Canberra, Australia)
- Organizing Committee
Dr. Shu-Kun Lin, MDPI AG, Basel, Switzerland
Dr. Franck Vazquez, MDPI AG, Basel, Switzerland
Ms. Connie Xiong, MDPI AG Branch Office, Wuhan, China
Keynote Speakers

1 Research Unit Nuclear Fusion, Department of Applied Physics, Ghent
University, Sint-Pietersnieuwstraat 41, B-9000 Ghent, Belgium
2 Laboratory for Plasma Physics, Royal Military Academy (ERM/KMS),
Renaissancelaan 30 Avenue de la Renaissance, B-1000 Brussels, Belgium
Geert Verdoolaege leads the group on Advanced Fusion Data Analysis at Ghent University. He has been working on various topics related to the foundations and applications of probability theory and machine learning methods since 1999. He was among the first to use various modern data analysis techniques in fusion science and he introduced the field at Ghent University. He first concentrated primarily on integrated data analysis for fusion diagnostics using Bayesian probability theory, later also including probabilistic modeling and analysis of textured images in remote sensing applications and functional brain scans obtained from magnetic resonance imaging. In addition, Geert Verdoolaege initiated research on pattern recognition in fusion data, modeled as probability distributions on information manifolds. His group develops new probabilistic techniques for analyzing highly stochastic fusion data and phenomena, with current applications to plasma instabilities (ELMs and disruptions), plasma turbulence and fusion scaling laws. Further activities include Bayesian analysis of fusion diagnostics with application to reflectometry and charge-exchange spectroscopy, and Bayesian real-time tomography for soft-X-ray spectroscopy.

Professor and Director
University at Buffalo, Buffalo, NY 14260, USA
Dr. Cemal Basaran is a Professor and the Director of Electronic Packaging Laboratory at University at Buffalo, The State University of New York. He specializes in computational and experimental damage mechanics of electronics materials. He has authored 135+ peer reviewed archival journal publications and several book chapters in the fields of damage mechanics of electronics packaging materials. His research includes but not limited to unification of Newtonian mechanics and thermodynamics using entropy, 2-D materials for power and nano electronics, electromigration, thermomigration, and computational fatigue life prediction without use of curve fitting models. Some of his awards include 1997 US Navy ONR Young Investigator Award, and 2011 ASME EPPD Excellence in Mechanics Award. He is a Fellow of the ASME. He has served and continues to serve on editorial board of 13 peer reviewed international journals, including IEEE Trans. on Advanced Packaging, IEEE Components, Packaging and Manufacturing Tech , ASME Journal of Electronic Packaging, ASCE Journal of Nanomechanics and Micromechanics, as well as numerous other journals. He has been the primary dissertation advisor to 24 PhD students.
His research has been funded by NSF, ONR, DoD, State of New York, and many industrial sponsors including but not limited to Northrop Grumman, Raytheon, Delphi, Intel, DuPont, Texas Instruments, Micron, Tyco Electronics, Analog Devices and many others. He serves as advisor to many national and international research funding agencies around the globe.

Istituto dei Sistemi Complessi (Consiglio Nazionale delle Ricerche),
p.le A. Moro 5, 00185 Roma, Italy
Dipartimento di Fisica, Sapienza University, p.le A. Moro 7, 00185 Roma,
Italy
Born in 1973, Ph. D. in Physics at Sapienza University (Rome) in 2002, from 2004 to 2005 postdoc Marie-Curie fellow at Paris-Sud University. After a few other postdocs at Sapienza University, I have passed the ERC Starting Grant 2007 selection with the "Granular Chaos" project which has been funded by Italian MIUR (ERC-MIUR agreement) in the period 2009-2014. In 2009 I got a permanent research position at Consiglio Nazionale delle Ricerche and I am now researcher at the Institute for Complex Systems (ISC) at CNR. I have been teaching the Course on Stochastic Processes at the Sapienza University (Physics Deparment) in the last 5 years. I have habilitation as Full Professor in Theoretical Physics (for fundamental interactions and for condensed matter). I've given about 50 talks (roughly 35 invited) at national and international conferences. I have been in the organising committee for 7 international conferences. I published more than 100 peer-reviewed articles in international journals, and a book ("Transport and fluctuations in granular fluids", Springer 2015). My scholar metrics states 3067 citations and h=32.

Universität zu Lübeck, Institut für Mathematik, 23562 Lübeck,
Schleswig-Holstein, Germany
Karsten Keller is working in time-discrete nonlinear dynamical systems and time series analysis with special emphasize on symbolic dynamics. The idea of coarse-graining is ubiquitous in his work reaching from combinatorial descriptions of dynamical systems to complexity quantification of time series and systems behind them. Recent research of Karsten Keller is mainly concentrated to the application of entropies and entropy-like measures to time series analysis, especially of ideas related to the relatively new concept of permutation entropy.

ARC DECRA Fellow and Senior Lecturer, Complex Systems Research Group and
Centre for Complex Systems, Faculty of Engineering and IT, The University
of Sydney, Sydney, NSW 2006, Australia
Dr. Joseph Lizier is an ARC DECRA fellow, and Senior Lecturer in Complex Systems, in the Faculty of Engineering and IT at The University of Sydney (since 2015). His research focusses on studying the dynamics of information processing in biological and bio-inspired complex systems and networks, in particular for neural systems. He is a developer of the JIDT toolbox for measuring the dynamics of complex systems using information theory, and the related IDTxl toolbox for inferring effective network structure in neural data. Before joining The University of Sydney, Dr. Lizier was a Research Scientist and Postdoctoral Fellow at CSIRO ICT Centre (Sydney, 2012-2014), and a Postdoctoral Researcher at the Max Planck Institute for Mathematics in the Sciences (Leipzig, 2010-2012). He has also worked as a Research Engineer in the telecommunications industry for 10 years, including at Seeker Wireless (2006-2010) and Telstra Research Laboratories (2001-2006). He obtained a PhD in Computer Science (2010), and Bachelor degrees in Electrical Engineering (2001) and Science (1999), from The University of Sydney.

Technical University Berlin, Faculty III of Process Sciences
Institute of Process, Engineering, Thermodynamics
Fasanenstr. 90, D-10623 Berlin, Germany
Interests: Irreversible and extended thermodynamics; Kinetic theory of gases; Shape memory alloys; Ferroelectricity; Phase transitions and phase diagrams; Hysteresis; Polyelectrolytic gels; Relativistic thermodynamics; Rubber and rubber balloons; Socio-thermodynamics; History of thermodynamics; Cosmology

retired from the Weierstrass Institute for Applied Analysis and Stochastics,
Mohrenstrasse 39, 10117 Berlin
Wolf Weiss received the Dipl. Ing. (M.S.) and the Ph.D. degrees from the Berlin University of Technology (TUB), Berlin, Germany, in 1985 and 1990, respectively. From 1985 to 1999, he worked as a Research Assistant with the Institute of Thermodynamics at the TUB, and received his Habilitation in thermodynamics in 1998. He is retired from the Weierstrass Institute for Applied Analysis and Stochastics, Berlin.
Interests: Irreversible, extended and relativistic thermodynamics; Kinetic theory of gases; Cosmology

Associate Professor, School of Mathematics, Centre for Complexity Sciences,
University of Bristol, Bristol, BS8 1TW, UK
Karoline Wiesner received a PhD in physics from Uppsala University, and has held postdoctoral positions at the Santa Fe Institute and at the University of California, Davis. Since 2007 she is faculty member of the School of Mathematics at the University of Bristol, where she also co-directs the Bristol Centre for Complexity Sciences. Her work focuses on information theoretic methods for applications in the sciences (e.g. protein dynamics, glass formers, stem cells), and on one foundations of complexity.

Director, Complex Systems Research Group, Faculty of Engineering and IT,
University of Sydney, NSW 2006, Australia
Director, Centre for Complex Systems, Faculty of Science, University of
Sydney, NSW 2006, Australia
List of Keynotes & Videos
USING ENTROPY TO UNNIFY MECHANICS AND THERMODYNAMIC: A NEW MECHANICS THEORY: MECHANO-THERMODYNAMICS
Related papers
Theory and Practice of Permutation Entropy
Related papers
Pattern recognition in nuclear fusion data by means of geiometric methods in probabilistic spaces
A. Statistical Physics
The main areas of interest of this section are: Statistical Mechanics, Irreversibility, Fluctuation Theorems, Equilibrium and Non-Equilibrium Distributions, Phase Transitions, Stochastic Systems, Chaos and Nonlinear Dynamics, Population Dynamics and Genetics.
This section is chaired by:
|
Dr. Antonio M. Scarfone |
| Prof. Dr. Miguel Rubi Secció de Física Estadística i Interdisciplinària - Departament de Física de la Matèria Condensada, Facultat de Física, Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain |
Session Chairs
Dr. Antonio Maria Scarfone, ISC-CNR
Professor J. Miguel Rubi
B. Information and Complexity
The main areas of interest of this section are: Simplicity and Complexity, Shannon Entropy, Kullback–Leibler Divergence, Channel Capacity, Alternative Entropies, Coding, Operations Research, Forecasting, Symmetry Breaking, Similarity.
This section is chaired by:
Prof. Dr. Raúl Alcaraz Martínez
Biomedical Engineering Research Group, Department of Electronic, University of Castilla-La Mancha, Campus
Universitario, 16071 Cuenca, Spain
Session Chair
Professor Raul Alcaraz, UCLM
C. Thermodynamics in Materials
The main areas of interest of this section are: Chemical thermodynamics, the Second Law, Free Energy, Enthalpy, Self-Organization, Biochemical Networks, Nano-Scale Physics, Molecular Theory of Fluids.
This section is chaired by:
Prof. Dr. Leslie Glasser
Nanochemistry Research Institute, Department of Chemistry, Curtin University, Perth 6845, West Australia
Session Chair
Professor Leslie Glasser, Curtin University
Show all published submissions (8) Hide published submissions (8)
Submissions
List of Papers (8) Toggle list
D. Quantum Information and Foundations
The main areas of interest of this section are: Quantum Foundations, Quantum Probability and non-Kolmogorov Models, Quantum-Like Models in Cognition, Decision Making, Psychology, Social and Political Science, Economics and Finances; Bell's Inequality, Quantum Nonlocality, Contextuality, Pure and Mixed States, Superposition, De-coherence, Quantum Computing, Born Rule and Generalizations, Causality and Randomness, Role of Conscious Observer.
This section is chaired by:
QUit Group, Department of Physics, University of Pavia, Pavia, Italy
Prof. Dr. Andrei Khrennikov
International Center for Mathematical Modeling in Physics, Engineering, Economics, and Cognitive Science, Linnaeus University, Växjö, Sweden
Session Chairs
Professor Giacomo D'ariano
Dr. Andrei Khrennikov
Show all published submissions (3) Hide published submissions (3)
Submissions
List of Papers (3) Toggle list
E. Machine Learning
The main areas of interest of this section are: Artificial Intelligence, Neural Networks, Cybernetics, Robotics, Man–Machine Interfaces, Bio-mimic Algorithms.
This section is chaired by:
Dr. Dawn E. Holmes
Department of Statistics and Applied Probability, University of California, USA
Prof. Dr. Alexander Gorban
Department of Mathematics, University of Leicester, Leicester LE1 7RH, UK
Session Chairs
Dr. Dawn Holmes
Professor Alexander Gorban
F. Astrophysics and Cosmology
The main areas of interest of this section are: Evolution of Stars, Gravitating Systems, Black Holes, The Universe.
This section is chaired by:
NASA Goddard Institute for Space Studies, 2880 Broadway, New York, NY 10027, USA
Session Chair
Dr. Michael J. Way, NASA Goddard Institute for Space Studies
P. Posters
In this section, posters can be presented stand-alone, i.e., without an accompanying proceedings paper or conference presentation. Posters will be available online on this website during and after the e-conference. However, posters will not be added to the proceedings of the conference.
This section is chaired by:
Prof. Phil Broadbridge
Department of Mathematics and Statistics, La Trobe University Melbourne, VIC 3086, Australia
Dr. Andriy Olenko
Department of Mathematics and Statistics, La Trobe University, Victoria, 3086, Australia
Session Chairs
Professor Philip Broadbridge
Dr. Andriy Olenko



















